Language mannequin coaching is sluggish, even when your mannequin just isn’t very massive. It is because you have to prepare the mannequin with a big dataset and there’s a massive vocabulary. Subsequently, it wants many coaching steps for the mannequin to converge. Nevertheless, there are some strategies recognized to hurry up the coaching course of. On this article, you’ll study them. Particularly, you’ll study:
- Utilizing optimizers
- Utilizing studying price schedulers
- Different strategies for higher convergence or decreased reminiscence consumption
Let’s get began.

How one can Pace-Up Coaching of Language Fashions
Picture by Emma Fabbri. Some rights reserved.
Overview
This text is split into 4 components; they’re:
- Optimizers for Coaching Language Fashions
- Studying Charge Schedulers
- Sequence Size Scheduling
- Different Methods to Assist Coaching Deep Studying Fashions
Optimizers for Coaching Language Fashions
Adam has been the preferred optimizer for coaching deep studying fashions. In contrast to SGD and RMSProp, Adam makes use of each the primary and second second of the gradient to replace the parameters. Utilizing the second second will help the mannequin converge quicker and extra stably, on the expense of utilizing extra reminiscence.
Nevertheless, when coaching language fashions these days, you’ll often use AdamW, the Adam optimizer with weight decay. Weight decay is a regularization method to forestall overfitting. It often entails including a small penalty to the loss perform. However in AdamW, the load decay is utilized on to the weights as an alternative. That is believed to be extra steady as a result of the regularization time period is decoupled from the calculated gradient. It is usually extra sturdy to hyperparameter tuning, because the impact of the regularization time period is utilized explicitly to the load replace.
In formulation, AdamW weight replace algorithm is as follows:
$$
start{aligned}
g_t &= nabla_theta L(theta_{t-1})
m_t &= beta_1 m_{t-1} + (1 – beta_1) g_t
v_t &= beta_2 v_{t-1} + (1 – beta_2) g_t^2
hat{m_t} &= m_t / (1 – beta_1^t)
hat{v_t} &= v_t / (1 – beta_2^t)
theta_t &= theta_{t-1} – alpha Huge( frac{hat{m_t}}{sqrt{hat{v_t}} + epsilon} + lambda theta_{t-1} Huge)
finish{aligned}
$$
The mannequin weight at step $t$ is denoted by $theta_t$. The $g_t$ is the computed gradient from the loss perform $L$, and $g_t^2$ is the elementwise sq. of the gradient. The $m_t$ and $v_t$ are the shifting common of the primary and second second of the gradient, respectively. Studying price $alpha$, weight decay $lambda$, and shifting common decay charges $beta_1$ and $beta_2$ are hyperparameters. A small worth $epsilon$ is used to keep away from division by zero. A standard alternative can be $beta_1 = 0.9$, $beta_2 = 0.999$, $epsilon = 10^{-8}$, and $lambda = 0.1$.
The important thing of AdamW is the $lambda theta_{t-1}$ time period within the gradient replace, as an alternative of within the loss perform.
AdamW just isn’t the one alternative of optimizer. Some newer optimizers have been proposed just lately, corresponding to Lion, SOAP, and AdEMAMix. You possibly can see the paper Benchmarking Optimizers for Massive Language Mannequin Pretraining for a abstract.
Studying Charge Schedulers
A studying price scheduler is used to regulate the training price throughout coaching. Often, you would like a bigger studying price for the early coaching steps and scale back the training price as coaching progresses to assist the mannequin converge. You possibly can add a warm-up interval to extend the training price from a small worth to the height over a brief interval (often 0.1% to 2% of whole steps), then the training price is decreased over the remaining coaching steps.
A warm-up interval often begins with a near-zero studying price and will increase linearly to the height studying price. A mannequin begins with randomized preliminary weights. Beginning with a big studying price may cause poor convergence, particularly for giant fashions, massive batches, and adaptive optimizers.
You possibly can see the necessity for warm-up from the equations above. Assume the mannequin is uncalibrated; the loss might differ tremendously between subsequent steps. Then the primary and second moments $m_t$ and $v_t$ can be fluctuating tremendously, and the gradient replace $theta_t – theta_{t-1}$ may even be fluctuating tremendously. Therefore, you would like the loss to be steady and transfer slowly in order that AdamW can construct a dependable working common. This may be simply achieved if $alpha$ is small.
On the studying price discount part, there are a couple of decisions:
- cosine decay: $LR = LR_{max} cdot frac12 Huge(1 + cos frac{pi t}{T}Huge)$
- square-root decay: $LR = LR_{max} cdot sqrt{frac{T – t}{T}}$
- linear decay: $LR = LR_{max} cdot frac{T – t}{T}$
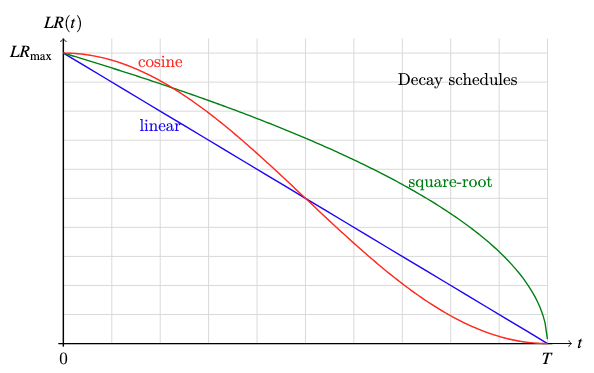
Plot of the three decay features
A big studying price will help the mannequin converge quicker whereas a small studying price will help the mannequin stabilize. Subsequently, you need the training price to be massive at the start when the mannequin remains to be uncalibrated, however small on the finish when the mannequin is near its optimum state. All decay schemes above can obtain this, however you wouldn’t need the training price to develop into “too small too quickly” or “too massive too late”. Cosine decay is the preferred alternative as a result of it drops the training price extra slowly at the start and stays longer at a low studying price close to the tip, that are fascinating properties to assist the mannequin converge quicker and stabilize respectively.
n PyTorch, you have got the CosineAnnealingLR scheduler to implement cosine decay. For the warm-up interval, you have to mix with the LinearLR scheduler. Beneath is an instance of the coaching loop utilizing AdamW, CosineAnnealingLR, and LinearLR:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
import torch import torch.nn as nn import torch.optim as optim from torch.optim.lr_scheduler import LinearLR, CosineAnnealingLR, SequentialLR
# Instance setup mannequin = torch.nn.Linear(10, 1) X, y = torch.randn(5, 10), torch.randn(5) loss_fn = nn.MSELoss() optimizer = optim.AdamW(mannequin.parameters(), lr=1e–2, betas=(0.9, 0.999), eps=1e–8, weight_decay=0.1)
# Outline studying price schedulers warmup_steps = 10 total_steps = 100 min_lr = 1e–4 warmup_lr = LinearLR(optimizer, start_factor=0.1, end_factor=1.0, total_iters=warmup_steps) cosine_lr = CosineAnnealingLR(optimizer, T_max=total_steps – warmup_steps, eta_min=min_lr) combined_lr = SequentialLR(optimizer, schedulers=[warmup_lr, cosine_lr], milestones=[warmup_steps])
# Coaching loop for step in vary(total_steps): # prepare one epoch y_pred = mannequin(X) loss = loss_fn(y_pred, y) # print loss and studying price print(f“Step {step+1}/{total_steps}: loss {loss.merchandise():.4f}, lr {combined_lr.get_last_lr()[0]:.4f}”) # backpropagate and replace weights optimizer.zero_grad() loss.backward() optimizer.step() combined_lr.step() |
Working this code, you might even see:
|
Step 1/100: loss 1.5982, lr 0.0010 Step 2/100: loss 1.5872, lr 0.0019 Step 3/100: loss 1.5665, lr 0.0028 … Step 9/100: loss 1.2738, lr 0.0082 Step 10/100: loss 1.2069, lr 0.0091 Step 11/100: loss 1.1387, lr 0.0100 … Step 98/100: loss 0.4845, lr 0.0001 Step 99/100: loss 0.4845, lr 0.0001 Step 100/100: loss 0.4845, lr 0.0001 |
Discover how the training price will increase after which decreases.
Sequence Size Scheduling
Language fashions are skilled with sequence information. Transformer fashions or recurrent neural networks are each architecturally agnostic to the sequence size. Nevertheless, it’s possible you’ll need to prepare the mannequin with lengthy sequence to let the mannequin discover ways to deal with lengthy context.
In coaching, lengthy sequence lengths may be problematic. First, you prepare with batches of sequences, and ragged lengths imply you have to pad the sequences to the utmost size within the batch. Whereas you’ll ignore the padded tokens, your mannequin nonetheless must course of them, therefore assets are wasted. Second, within the consideration mechanism, the complexity is quadratic to the sequence size. The longer the sequence, the extra pricey it’s to course of.
Subsequently, it’s possible you’ll need to create batches with sequences of comparable size to keep away from extreme padding.
You might also need to prepare the mannequin with shorter sequences first. You possibly can velocity up the coaching course of by shortly forcing the mannequin to study the patterns of the language utilizing shorter sequences. As soon as the mannequin has pretty converged, you’ll be able to step by step improve the sequence size to assist the mannequin discover ways to deal with lengthy contexts.
These are widespread strategies in coaching massive language fashions to save lots of computational assets. Notice that you just nonetheless arrange the mannequin with a set most sequence size, which impacts the way you configure the positional embeddings. Nevertheless, you don’t exhaust the utmost sequence size till the mannequin has pretty converged.
Implementing sequence size scheduling means you have to write a extra advanced information loader to take into consideration of the present epoch to return the suitable coaching information.
Different Methods to Assist Coaching Deep Studying Fashions
Random Restart
Coaching a deep studying mannequin is a fancy course of and never straightforward to get proper, particularly for big fashions. One widespread problem is the mannequin getting caught in an area minimal and being unable to converge. Utilizing momentum in gradient descent will help the mannequin escape from native minima, however just isn’t at all times efficient. One other strategy is to easily restart the coaching if you happen to ever see the mannequin fail to converge.
Random restart is the technique of coaching the mannequin a number of instances from scratch. It makes use of completely different random seeds every time in order that the mannequin begins with completely different preliminary weights and completely different shuffling of the info. That is performed within the hope that you’ll not at all times get caught in the identical native minimal, so you’ll be able to decide the one with the most effective efficiency. That is preferrred if you happen to can prepare a number of fashions for fewer epochs at the start, then decide the most effective mannequin from the pool to complete coaching with extra epochs.
Gradient Clipping
One widespread problem in coaching deep studying fashions is gradient explosion. That is particularly widespread if you happen to prepare the mannequin utilizing lower-precision floating-point numbers, wherein the vary of the gradient could possibly be too massive to be represented. Gradient clipping is the strategy of limiting the magnitude of the gradient to a secure worth. With out it, you might even see your coaching course of abruptly fail because of the mannequin weights or loss perform turning into NaN or infinity.
There are a number of methods to clip gradients. The commonest one is to clip the gradient such that the L2 norm is lower than a secure worth, corresponding to 1.0 or 6.0. You may also clip the gradient to a price vary, corresponding to -5.0 to five.0.
Gradient clipping by L2 norm means scaling the complete gradient vector if the L2 norm $Vert g_t Vert_2$ is bigger than a secure worth $c$:
$$
hat{g_t} = minbig(1, frac{c}{Vert g_t Vert_2}huge) cdot g_t
$$
However, gradient clipping by worth means setting the gradient to a secure worth every time the gradient exceeds that worth:
$$
hat{g_t} = start{circumstances}
-c & textual content{if } g_t
g_t & textual content{if } -c le g_t le c
c & textual content{if } g_t > c
finish{circumstances}
$$
Utilizing gradient clipping in PyTorch is easy. You need to use the torch.nn.utils.clip_grad_norm_ perform to clip the gradient by L2 norm, or the torch.nn.utils.clip_grad_value_ perform to clip the gradient by worth. Beneath is an instance:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
import torch import torch.nn as nn import torch.optim as optim from torch.nn.utils import clip_grad_norm_, clip_grad_value_
# Instance setup mannequin = torch.nn.Linear(10, 1) X, y = torch.randn(5, 10), torch.randn(5) total_steps = 100 loss_fn = nn.MSELoss() optimizer = optim.AdamW(mannequin.parameters(), lr=1e–2, betas=(0.9, 0.999), eps=1e–8, weight_decay=0.1)
# Coaching loop for step in vary(total_steps): # prepare one epoch y_pred = mannequin(X) loss = loss_fn(y_pred, y) optimizer.zero_grad() loss.backward() # clip by L2 norm clip_grad_norm_(mannequin.parameters(), max_norm=1.0) # or clip by worth # clip_grad_value_(mannequin.parameters(), clip_value=1.0) optimizer.step() |
Blended Precision Coaching
When a mannequin turns into too massive, reminiscence consumption turns into a bottleneck as nicely. It’s possible you’ll need to save reminiscence through the use of lower-precision floating-point numbers in coaching, corresponding to half precision (float16) or bfloat16. In comparison with single precision (float32), float16 and bfloat16 can scale back reminiscence consumption by half, however the vary and precision are sacrificed.
Subsequently, it’s possible you’ll need to use blended precision coaching, wherein a part of the mannequin makes use of float32 whereas the opposite half makes use of float16. A standard alternative is to make use of float32 for biases however float16 for weights in linear layers.
Fashionable GPUs can run float16 operations on the identical velocity as float32, however since you’ll be able to function on extra information on the identical time, you’ll be able to successfully run the coaching course of at double velocity.
Additional Readings
Beneath are some assets that you could be discover helpful:
Abstract
On this article, you discovered about some strategies to hurry up the coaching means of deep studying fashions, particularly for big language fashions. Particularly, you discovered that:
- AdamW with cosine decay is the preferred optimizer and studying price scheduler for coaching language fashions.
- You need to use sequence size scheduling to save lots of computational assets when coaching language fashions.
- Methods like random restart and gradient clipping will help you prepare the mannequin extra stably.
- Blended precision coaching will help you scale back reminiscence consumption.


