Calibration Curves in Analytical Chemistry: Ideas, Process, and Functions

Calibration curves are important instruments in analytical chemistry, biochemistry, and pharmaceutical evaluation. They assist perceive the instrumental response to an analyte and predict the focus of unknown samples precisely. This text offers an in depth, student-friendly information to calibration curves, together with ideas, preparation, plotting, and purposes.

What Is a Calibration Curve?

A calibration curve is a graph that relates the instrumental sign (response) to the identified concentrations of a regular analyte. By measuring a number of customary options, a relationship is established, which may then be used to find out the focus of an unknown pattern.

• Customary options are ready at completely different concentrations protecting the anticipated vary of the unknown pattern.

• Repeated measurements permit for the calculation of error bars, serving to estimate experimental variability.

• Sometimes, the response is linear, however non-linear capabilities may also be used if the perform is thought.

Ideas of Calibration Curves

1. Matrix Consideration: Ideally, customary samples needs to be run in the identical matrix because the unknown pattern. The matrix contains all parts besides the analyte, resembling salts, proteins, or solvents. When precise matching isn’t doable, an approximate matrix can be utilized (e.g., synthetic urine or synthetic cerebrospinal fluid).

2. Linearity: Many calibration curves observe the linear equation:

   y = mx + b

   • m: slope (sensitivity of the measurement)

   • b: y-intercept

   • Linear regression offers an R² worth, indicating how intently knowledge match the road (R² > 0.95 is good).

3. Linear Vary and Sensitivity: The slope represents sensitivity. A steep slope signifies the instrument responds strongly to small modifications in focus. The linear vary is the vary over which the instrument offers a dependable linear response. Past this vary, the response could plateau.

4. Limits:

   • Restrict of Detection (LOD): Minimal quantity detectable above noise. Calculated as LOD = 3 × S.D./m.

   • Restrict of Quantitation (LOQ): Minimal quantity measurable with acceptable precision. LOQ = 10 × S.D./m.

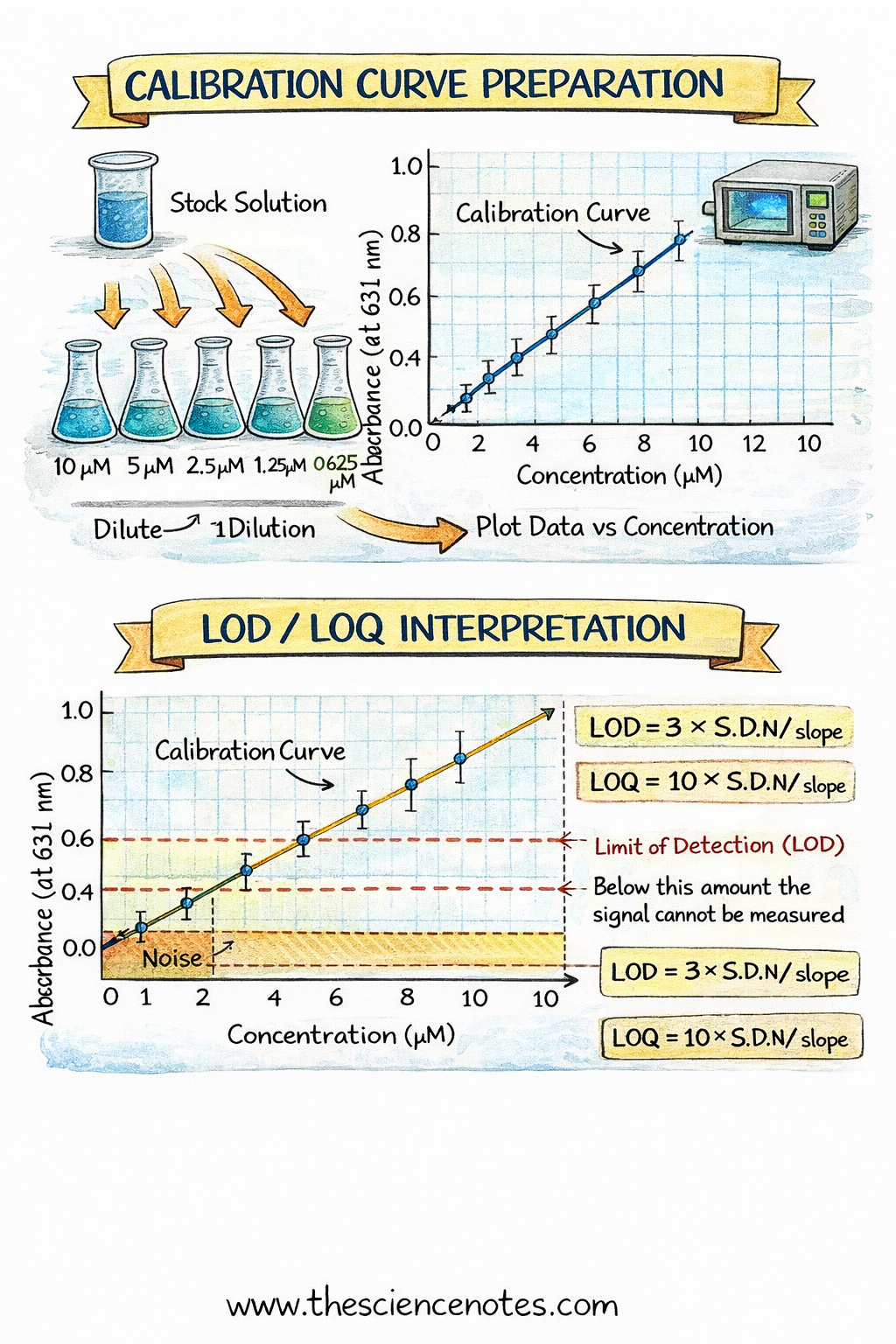
Process: Making ready a Calibration Curve

1. Making Requirements Utilizing Serial Dilutions

• Put together a concentrated inventory resolution by precisely weighing the analyte and dissolving it in solvent.

• Carry out serial dilutions to generate a sequence of decrease concentrations:

  • Dilute the inventory resolution stepwise into volumetric flasks.

  • Hold the dilution issue fixed (e.g., 10-fold dilutions).

• A minimum of 5 concentrations are beneficial for a dependable curve.

• Notice: Any pipetting errors propagate via serial dilutions, so cautious approach is crucial.

2. Measuring Instrumental Response

• Measure the response of every customary utilizing an acceptable instrument (e.g., UV-Vis spectrophotometer, ion-selective electrode).

• Take a number of readings (3–5 repeats) to estimate noise and enhance accuracy.

• Measure the unknown pattern beneath similar situations because the requirements.

3. Plotting the Calibration Curve

• Enter focus vs. sign knowledge right into a spreadsheet.

• Embrace error bars if repeated measurements had been taken.

• Match the information to a linear or identified non-linear perform.

• Use linear regression to calculate slope (m), intercept (b), and R².

• Determine the linear portion and exclude outlier factors solely on the edges, not in the midst of the curve.

4. Calculating Unknown Focus, LOD, and LOQ

• Use the calibration curve equation to find out the unknown focus.

• Calculate LOD and LOQ utilizing the slope and customary deviation of noise.

• Dilute samples in the event that they exceed the linear vary of the instrument.

Instance: UV-Vis Calibration of Blue Dye #1

• Measured absorbance of 0–10 µM blue dye at 631 nm.

• Linear regression gave: y = 0.109x + 0.0286, R² > 0.99.

• Noise customary deviation: 0.021

• LOD = 0.58 µM, LOQ = 1.93 µM

• Unknown pattern absorbance = 0.243 → focus = 2.02 µM (earlier than dilution correction)

Functions of Calibration Curves

Calibration curves are extensively used throughout numerous fields:

• Environmental Evaluation: Figuring out pollution in water or soil samples.

• Biochemistry: Measuring neurotransmitters or proteins in organic fluids.

• Prescription drugs: Quantifying nutritional vitamins, medicine, or components.

• Meals Science: Analyzing caffeine, dyes, or vitamins in drinks and meals.

• Electrochemistry: Utilizing ion-selective electrodes to quantify ions (e.g., fluoride) with log-scale calibration curves following the Nernst equation.

Ideas for Correct Calibration

• Use a matrix that intently resembles the unknown pattern.

• Carry out a number of measurements for every focus to estimate noise.

• Guarantee concentrations bracket the anticipated vary of unknowns.

• Deal with pipettes, balances, and volumetric flasks fastidiously to scale back error propagation.

• Use software program for plotting, regression, and error evaluation.

Conclusion

Calibration curves are foundational in analytical chemistry. They permit researchers to predict unknown concentrations, calculate detection limits, and consider instrument sensitivity. By fastidiously making ready requirements, working correct measurements, and analyzing knowledge appropriately, calibration curves grow to be a dependable instrument for environmental, organic, pharmaceutical, and meals science purposes.