On this article, you’ll study three dependable methods — ordinal encoding, one-hot encoding, and goal (imply) encoding — for turning categorical options into model-ready numbers whereas preserving their which means.
Subjects we’ll cowl embrace:
- When and easy methods to apply ordinal (label-style) encoding for actually ordered classes.
- Utilizing one-hot encoding safely for nominal options and understanding its trade-offs.
- Making use of goal (imply) encoding for high-cardinality options with out leaking the goal.
Time to get to work.
3 Sensible Methods to Encode Categorical Options for Machine Studying
Picture by Editor
Introduction
In case you spend any time working with real-world knowledge, you rapidly notice that not all the things is available in neat, clear numbers. In truth, a lot of the attention-grabbing points, the issues that outline folks, locations, and merchandise, are captured by classes. Take into consideration a typical buyer dataset: you’ve obtained fields like Metropolis, Product Sort, Schooling Stage, and even Favourite Shade. These are all examples of categorical options, that are variables that may tackle considered one of a restricted, fastened variety of values.
The issue? Whereas our human brains seamlessly course of the distinction between “Pink” and “Blue” or “New York” and “London,” the machine studying fashions we use to make predictions can’t. Fashions like linear regression, resolution bushes, or neural networks are essentially mathematical capabilities. They function by multiplying, including, and evaluating numbers. They should calculate distances, slopes, and possibilities. While you feed a mannequin the phrase “Advertising and marketing,” it doesn’t see a job title; it simply sees a string of textual content that has no numerical worth it will possibly use in its equations. This incapacity to course of textual content is why your mannequin will crash immediately if you happen to attempt to prepare it on uncooked, non-numeric labels.
The first aim of function engineering, and particularly encoding, is to behave as a translator. Our job is to transform these qualitative labels into quantitative, numerical options with out shedding the underlying which means or relationships. If we do it proper, the numbers we create will carry the predictive energy of the unique classes. As an example, encoding should make sure that the quantity representing a high-level Schooling Stage is quantitatively “greater” than the quantity representing a decrease degree, or that the numbers representing totally different Cities replicate their distinction in buy habits.
To sort out this problem, now we have developed good methods to carry out this translation. We’ll begin with essentially the most intuitive strategies, the place we merely assign numbers primarily based on rank or create separate binary flags for every class. Then, we’ll transfer on to a strong method that makes use of the goal variable itself to construct a single, dense function that captures a class’s true predictive affect. By understanding this development, you’ll be outfitted to decide on the proper encoding methodology for any categorical knowledge you encounter.
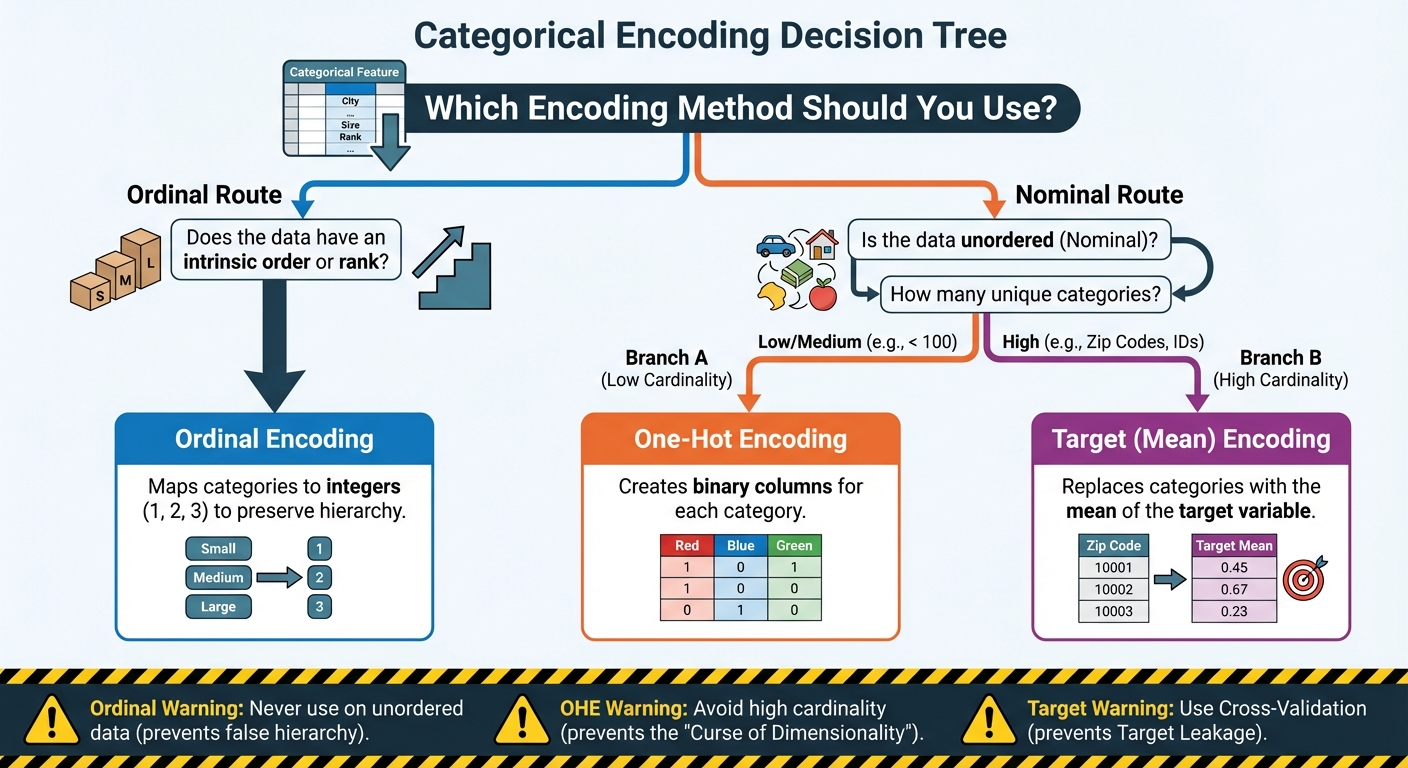
3 Sensible Methods to Encode Categorical Options for Machine Studying: A Flowchart (click on to enlarge)
Picture by Editor
1. Preserving Order: Ordinal and Label Encoding
The primary, and easiest, translation method is designed for categorical knowledge that isn’t only a assortment of random names, however a set of labels with an intrinsic rank or order. That is the important thing perception. Not all classes are equal; some are inherently “greater” or “extra” than others.
The most typical examples are options that characterize some kind of scale or hierarchy:
- Schooling Stage: (Excessive Faculty => School => Grasp’s => PhD)
- Buyer Satisfaction: (Very Poor => Poor => Impartial => Good => Wonderful)
- T-shirt Measurement: (Small => Medium => Massive)
While you encounter knowledge like this, the simplest method to encode it’s to make use of Ordinal Encoding (typically informally referred to as “label encoding” when mapping classes to integers).
The Mechanism
The method is simple: you map the classes to integers primarily based on their place within the hierarchy. You don’t simply assign numbers randomly; you explicitly outline the order.
For instance, you probably have T-shirt sizes, the mapping would seem like this:
| Authentic Class | Assigned Numerical Worth |
|---|---|
| Small (S) | 1 |
| Medium (M) | 2 |
| Massive (L) | 3 |
| Additional-Massive (XL) | 4 |
By doing this, you might be instructing the machine that an XL (4) is numerically “extra” than an S (1), which appropriately displays the real-world relationship. The distinction between an M (2) and an L (3) is mathematically the identical because the distinction between an L (3) and an XL (4), a unit enhance in dimension. This ensuing single column of numbers is what you feed into your mannequin.
Introducing a False Hierarchy
Whereas Ordinal Encoding is the proper selection for ordered knowledge, it carries a serious threat when misapplied. You could by no means apply it to nominal (non-ordered) knowledge.
Contemplate encoding a listing of colours: Pink, Blue, Inexperienced. In case you arbitrarily assign them: Pink = 1, Blue = 2, Inexperienced = 3, your machine studying mannequin will interpret this as a hierarchy. It can conclude that “Inexperienced” is twice as giant or vital as “Pink,” and that the distinction between “Blue” and “Inexperienced” is similar because the distinction between “Pink” and “Blue.” That is nearly actually false and can severely mislead your mannequin, forcing it to study non-existent numerical relationships.
The rule right here is easy and agency: use Ordinal Encoding solely when there’s a clear, defensible rank or sequence between the classes. If the classes are simply names with none intrinsic order (like sorts of fruit or cities), you should use a distinct encoding method.
Implementation and Code Rationalization
We are able to implement this utilizing the OrdinalEncoder from scikit-learn. The hot button is that we should explicitly outline the order of the classes ourselves.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
from sklearn.preprocessing import OrdinalEncoder import numpy as np
# Pattern knowledge representing buyer schooling ranges knowledge = np.array([[‘High School’], [‘Bachelor’s’], [‘Master’s’], [‘Bachelor’s’], [‘PhD’]])
# Outline the specific order for the encoder # This ensures that ‘Bachelor’s’ is appropriately ranked under ‘Grasp’s’ education_order = [ [‘High School’, ‘Bachelor’s’, ‘Master’s’, ‘PhD’] ]
# Initialize the encoder and go the outlined order encoder = OrdinalEncoder(classes=education_order)
# Match and rework the information encoded_data = encoder.fit_transform(knowledge)
print(“Authentic Information:n”, knowledge.flatten()) print(“nEncoded Information:n”, encoded_data.flatten()) |
Within the code above, the vital half is setting the classes parameter when initializing OrdinalEncoder. By passing the precise record education_order, we inform the encoder that ‘Excessive Faculty’ comes first, then ‘Bachelor’s’, and so forth. The encoder then assigns the corresponding integers (0, 1, 2, 3) primarily based on this practice sequence. If we had skipped this step, the encoder may need assigned the integers primarily based on alphabetical order, which might destroy the significant hierarchy we wished to protect.
2. Eliminating Rank: One-Scorching Encoding (OHE)
As we mentioned, Ordinal Encoding solely works in case your classes have a transparent rank. However what about options which might be purely nominal, which means they’ve names, however no inherent order? Take into consideration issues like Nation, Favourite Animal, or Gender. Is “France” higher than “Japan”? Is “Canine” mathematically higher than “Cat”? Completely not.
For these non-ordered options, we want a method to encode them numerically with out introducing a false sense of hierarchy. The answer is One-Scorching Encoding (OHE), which is by far essentially the most extensively used and most secure encoding method for nominal knowledge.
The Mechanism
The core concept behind OHE is easy: as a substitute of changing a single class column with a single quantity, it’s changed with a number of binary columns. For each distinctive class in your unique function, you create a brand-new column. These new columns are sometimes referred to as dummy variables.
For instance, in case your unique Shade function has three distinctive classes (Pink, Blue, Inexperienced), OHE will create three new columns: Color_Red, Color_Blue, and Color_Green.
In any given row, solely a type of columns will likely be “scorching” (a price of 1), and the remaining will likely be 0.
| Authentic Shade | Color_Red | Color_Blue | Color_Green |
|---|---|---|---|
| Pink | 1 | 0 | 0 |
| Blue | 0 | 1 | 0 |
| Inexperienced | 0 | 0 | 1 |
This methodology is sensible as a result of it utterly solves the hierarchy drawback. The mannequin now treats every class as a very separate, unbiased function. “Blue” is now not numerically associated to “Pink”; it simply exists in its personal binary column. That is the most secure and most dependable default selection when you already know your classes don’t have any order.
The Commerce-off
Whereas OHE is the usual for options with low to medium cardinality (i.e., a small to average variety of distinctive values, usually underneath 100), it rapidly turns into an issue when coping with high-cardinality options.
Cardinality refers back to the variety of distinctive classes in a function. Contemplate a function like Zip Code in the USA, which might simply have over 40,000 distinctive values. Making use of OHE would power you to create 40,000 brand-new binary columns. This results in two main points:
- Dimensionality: You instantly balloon the width of your dataset, creating an enormous, sparse matrix (a matrix containing principally zeros). This dramatically slows down the coaching course of for many algorithms.
- Overfitting: Many classes will solely seem a couple of times in your dataset. The mannequin may assign an excessive weight to considered one of these uncommon, particular columns, primarily memorizing its one look slightly than studying a basic sample.
When a function has 1000’s of distinctive classes, OHE is just impractical. This limitation forces us to look past OHE and leads us on to our third, extra superior method for coping with knowledge at an enormous scale.
Implementation and Code Rationalization
In Python, the OneHotEncoder from scikit-learn or the get_dummies() perform from pandas are the usual instruments. The pandas methodology is usually simpler for fast transformation:
|
import pandas as pd
# Pattern knowledge with a nominal function: Shade knowledge = pd.DataFrame({ ‘ID’: [1, 2, 3, 4, 5], ‘Shade’: [‘Red’, ‘Blue’, ‘Red’, ‘Green’, ‘Blue’] })
# 1. Apply One-Scorching Encoding utilizing pandas get_dummies df_encoded = pd.get_dummies(knowledge, columns=[‘Color’], prefix=‘Is’)
print(df_encoded) |
On this code, we go our DataFrame knowledge and specify the column we need to rework (Shade). The prefix='Is' merely provides a clear prefix (like ‘Is_Red‘) to the brand new columns for higher readability. The output DataFrame retains the ID column and replaces the only Shade column with three new, unbiased binary options: Is_Red, Is_Blue, and Is_Green. A row that was initially ‘Pink’ now has a 1 within the Is_Red column and a 0 within the others, attaining the specified numerical separation with out imposing rank.
3. Harnessing Predictive Energy: Goal (Imply) Encoding
As we established, One-Scorching Encoding fails spectacularly when a function has excessive cardinality, 1000’s of distinctive values like Product ID, Zip Code, or E-mail Area. Creating 1000’s of sparse columns is computationally inefficient and results in overfitting. We want a way that may compress these 1000’s of classes right into a single, dense column with out shedding their predictive sign.
The reply lies in Goal Encoding, additionally regularly referred to as Imply Encoding. As an alternative of relying solely on the function itself, this methodology strategically makes use of the goal variable (Y) to find out the numerical worth of every class.
The Idea and Mechanism
The core concept is to encode every class with the typical worth of the goal variable for all knowledge factors belonging to that class.
As an example, think about you are attempting to foretell if a transaction is fraudulent (Y=1 for fraud, Y=0 for official). In case your categorical function is Metropolis:
- You group all transactions by Metropolis
- For every metropolis, you calculate the imply of the Y variable (the typical fraud charge)
- The town of “Miami” may need a mean fraud charge of 0.10 (or 10%), and “Boston” may need 0.02 (2%)
- You exchange the specific label “Miami” in each row with the quantity 0.10, and “Boston” with 0.02
The result’s a single, dense numerical column that instantly embeds the predictive energy of that class. The mannequin immediately is aware of that rows encoded with 0.10 are ten instances extra more likely to be fraudulent than rows encoded with 0.01. This drastically reduces dimensionality whereas maximizing data density.
The Benefit and The Essential Hazard
The benefit of Goal Encoding is evident: it solves the high-cardinality drawback by changing 1000’s of sparse columns with only one dense, highly effective function.
Nonetheless, this methodology is usually referred to as “essentially the most harmful encoding method” as a result of this can be very weak to Goal Leakage.
Goal leakage happens if you inadvertently embrace data in your coaching knowledge that will not be obtainable at prediction time, resulting in artificially excellent (and ineffective) mannequin efficiency.
The Deadly Mistake: In case you calculate the typical fraud charge for Miami utilizing all the information, together with the row you might be at present encoding, you might be leaking the reply. The mannequin learns an ideal correlation between the encoded function and the goal variable, primarily memorizing the coaching knowledge as a substitute of studying generalizable patterns. When deployed on new, unseen knowledge, the mannequin will fail spectacularly.
Stopping Leakage
To make use of Goal Encoding safely, you should make sure that the goal worth for the row being encoded isn’t used within the calculation of its function worth. This requires superior methods:
- Cross-Validation (Okay-Fold): Essentially the most strong strategy is to make use of a cross-validation scheme. You break up your knowledge into Okay folds. When encoding one fold (the “holdout set”), you calculate the goal imply solely utilizing the information from the opposite Okay-1 folds (the “coaching set”). This ensures the function is generated from out-of-fold knowledge.
- Smoothing: For classes with only a few knowledge factors, the calculated imply will be unstable. Smoothing is utilized to “shrink” the imply of uncommon classes towards the worldwide common of the goal variable, making the function extra strong. A standard smoothing components typically includes weighting the class imply with the worldwide imply primarily based on the pattern dimension.
Implementation and Code Rationalization
Implementing secure Goal Encoding often requires customized capabilities or superior libraries like category_encoders, as scikit-learn’s core instruments don’t supply built-in leakage safety. The important thing precept is calculating the means exterior of the first knowledge being encoded.
For demonstration, we’ll use a conceptual instance, specializing in the results of the calculation:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
import pandas as pd
# Pattern knowledge knowledge = pd.DataFrame({ ‘Metropolis’: [‘Miami’, ‘Boston’, ‘Miami’, ‘Boston’, ‘Boston’, ‘Miami’], # Goal (Y): 1 = Fraud, 0 = Authentic ‘Fraud_Target’: [1, 0, 1, 0, 0, 0] })
# 1. Calculate the uncooked imply (for demonstration solely — that is UNSAFE leakage) # Actual-world use requires out-of-fold means for security! mean_encoding = knowledge.groupby(‘Metropolis’)[‘Fraud_Target’].imply().reset_index() mean_encoding.columns = [‘City’, ‘City_Encoded_Value’]
# 2. Merge the encoded values again into the unique knowledge df_encoded = knowledge.merge(mean_encoding, on=‘Metropolis’, how=‘left’)
# Output the calculated means for illustration miami_mean = df_encoded[df_encoded[‘City’] == ‘Miami’][‘City_Encoded_Value’].iloc[0] boston_mean = df_encoded[df_encoded[‘City’] == ‘Boston’][‘City_Encoded_Value’].iloc[0]
print(f“Miami Encoded Worth: {miami_mean:.4f}”) print(f“Boston Encoded Worth: {boston_mean:.4f}”) print(“nFinal Encoded Information (Conceptual Leakage Instance):n”, df_encoded) |
On this conceptual instance, “Miami” has three information with goal values [1, 1, 0], giving a mean (imply) of 0.6667. “Boston” has three information [0, 0, 0], giving a mean of 0.0000. The uncooked metropolis names are changed by these float values, dramatically rising the function’s predictive energy. Once more, to make use of this in an actual venture, the City_Encoded_Value would must be calculated rigorously utilizing solely the subset of knowledge not being educated on, which is the place the complexity lies.
Conclusion
We’ve lined the journey of reworking uncooked, summary classes into the numerical language that machine studying fashions demand. The distinction between a mannequin that works and one which excels typically comes right down to this function engineering step.
The important thing takeaway is that no single method is universally superior. As an alternative, the precise selection relies upon solely on the character of your knowledge and the variety of distinctive classes you might be coping with.
To rapidly summarize the three good approaches we’ve detailed:
- Ordinal Encoding: That is your answer when you have got an intrinsic rank or hierarchy amongst your classes. It’s environment friendly, including just one column to your dataset, but it surely should be reserved completely for ordered knowledge (like sizes or ranges of settlement) to keep away from introducing deceptive numerical relationships.
- One-Scorching Encoding (OHE): That is the most secure default when coping with nominal knowledge the place order doesn’t matter and the variety of classes is small to medium. It prevents the introduction of false rank, however you should be cautious of utilizing it on options with 1000’s of distinctive values, as it will possibly balloon the dataset dimension and decelerate coaching.
- Goal (Imply) Encoding: That is the highly effective reply for high-cardinality options that will overwhelm OHE. By encoding the class with its imply relationship to the goal variable, you create a single, dense, and extremely predictive function. Nonetheless, as a result of it makes use of the goal variable, it calls for excessive warning and should be carried out utilizing cross-validation or smoothing to forestall catastrophic goal leakage.


